In engineering and physics, the study of transport phenomena concerns the exchange of mass, energy, or momentum between observed and studied engineering systems. This subject is a fundamental component of disciplines involved with fluid mechanics, heat transfer, and mass transfer.
Transport phenomena actually encompasses all agents of physical change in the universe
It is now considered to be a part of the engineering discipline as much as thermodynamics, mechanics, and electromagnetism. Momentum, heat (energy), and mass transport share a similar mathematical framework, and a similar analytical mechanism that carries out the exchange process.
Transport phenomena actually encompasses all agents of physical change in the universe. Moreover, it is considered to be fundamental building block which developed the universe, and which is responsible for the success of all life on earth. However, the scope here limits the transport phenomena to its relationship to artificial engineered systems.
In physics, transport phenomena are all irreversible processes of statistical nature stemming from the random continuous motion of molecules, mostly observed in fluids. They involve a net macroscopic transfer of matter, energy or momentum in thermodynamic systems that are not in statistical equilibrium. Examples of transport processes include heat conduction (energy transfer), viscosity (momentum transfer), molecular diffusion (mass transfer), radiation and electric charge transfer in semiconductors.
Transport phenomena have wide application. For example, in solid state physics, the motion and interaction of electrons, holes and phonons are studied under “transport phenomena”. Another example is in biomedical engineering, where some transport phenomena of interest are thermoregulation, perfusion, and microfluidics. In chemical engineering, transport phenomena are studied in reactor design, analysis of molecular or diffusive transport mechanisms, and metallurgy.
The transport of mass, energy, and momentum can be affected by the presence of external sources:
- An odour dissipates more slowly when the source of the odor remains present.
- The rate of cooling of a solid that is conducting heat depends on whether a heat source is applied.
- The gravitational force acting on a rain drop counteracts the drag imparted by the surrounding air.
Diffusion
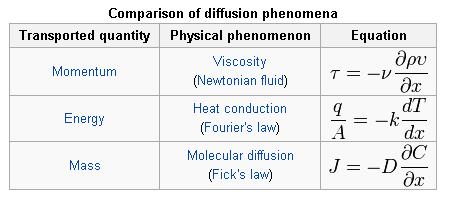
There are some notable similarities in equations for momentum, energy, and mass transfer which can all be transported by diffusion, as illustrated by the following examples :
- Mass : the spreading and dissipation of odours in air is an example of mass diffusion.
- Energy : the conduction of heat in a solid material is an example of heat diffusion.
- Momentum : the drag experienced by a rain drop as it falls in the atmosphere is an example of momentum diffusion (the rain drop loses momentum to the surrounding air through viscous stresses and decelerates).
The molecular transfer equations of Newton’s law for fluid momentum, Fourier’s law for heat, and Fick’s law for mass are very similar. One can convert from one transfer coefficient to another in order to compare all three different transport phenomena.
A great deal of effort has been devoted in the literature to developing analogies among these three transport processes for turbulent transfer so as to allow prediction of one from any of the others. The Reynolds analogy assumes that the turbulent diffusivities are all equal and that the molecular diffusivities of momentum (µ/p) and mass (DAB) are negligible compared to the turbulent diffusivities. When liquids are present and/or drag is present, the analogy is not valid. Other analogies, such as von Karman’s and Prandtl’s, usually result in poor relations.
The most successful and most widely used analogy is the Chilton and Colburn J-factor analogy. This analogy is based on experimental data for gases and liquids in both the laminar and turbulent regimes. Although it is based on experimental data, it can be shown to satisfy the exact solution derived from laminar flow over a flat plate. All of this information is used to predict transfer of mass.
In fluid systems described in terms of temperature, matter density, and pressure, it is known that temperature differences lead to heat flows from the warmer to the colder parts of the system; similarly, pressure differences will lead to matter flow from high-pressure to low-pressure regions (a “reciprocal relation”). What is remarkable is the observation that, when both pressure and temperature vary, temperature differences at constant pressure can cause matter flow (as in convection) and pressure differences at constant temperature can cause heat flow. Perhaps surprisingly, the heat flow per unit of pressure difference and the density (matter) flow per unit of temperature difference are equal.
This equality was shown to be necessary by Lars Onsager using statistical mechanics as a consequence of the time reversibility of microscopic dynamics. The theory developed by Onsager is much more general than this example and capable of treating more than two thermodynamic forces at once.
Momentum Transfer
In momentum transfer, the fluid is treated as a continuous distribution of matter. The study of momemtum transfer, or fluid mechanics can be divided into two branches: fluid statics (fluids at rest), and fluid dynamics (fluids in motion). When a fluid is flowing in the x direction parallel to a solid surface, the fluid has x-directed momentum, and its concentration is vxp. By random diffusion of molecules there is an exchange of molecules in the z direction. Hence the x-directed momentum has been transferred in the z-direction from the faster- to the slower-moving layer. The equation for momentum transport is Newton’s Law of Viscosity written as follows :
where Tzx is the flux of x-directed momentum in the z direction, v is µ/p, the momentum diffusivitym z is the distance of transport or diffusion, p is the density, and v is the viscosity. Newtons Law is the simplest relationship between the flux of momentum and the velocity gradient.
Mass Transfer
When a system contains two or more components whose concentration vary from point to point, there is a natural tendency for mass to be transferred, minimizing any concentration difference within the system. Mass Transfer in a system is governed by Fick’s First Law: ‘Diffusion flux from higher concentration to lower concentration is proportional to the gradient of the concentration of the substance and the diffusivity of the substance in the medium.’ Mass transfer can take place due to different driving forces. Some of them are :
- Mass can be transferred by the action of a pressure gradient(pressure diffusion)
- Forced diffusion occurs because of the action of some external force
- Diffusion is caused by temperature gradients (thermal diffusion)
This can be compared to Fourier’s Law for conduction of heat :
where D is the diffusivity constant.
Energy Transfer
All process in engineering involve the transfer of energy. Some examples are the heating and cooling of process streams, phase changes, distillations, etc. The basic principle is the law of thermodynamic which is expressed as follows for a static system :
For other systems that involve either turbulent flow, complex geometries or difficult boundary conditions another equation would be easier to use :
where A is the surface area, delta T is the temperature driving force, q is the heat flow per unit time, and h is the heat transfer coefficient.
Within heat transfer, two types of convection can occur. Forced convection can occur in both laminar and turbulent flow. In the situation of laminar flow in circular tubes, several dimensionless numbers are used such as Nusselt number, Reynolds number, and Prandlt. The commonly used equation is :
Natural or free convection is a function of Grashof and Prandlt numbers. The complexities of free convection heat transfer make it necessary to mainly use empirical relations from experimental data. Heat transfer is analyzed in packed beds, reactors and heat exchangers.
You might also like
 |
 |
 |
 |
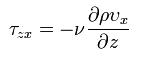
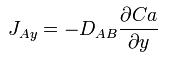
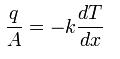
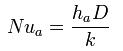
Alloy Suppliers
Aluminum
Aluminum Extrusions
Copper-Brass-Bronze
Nickel
Magnets
Stainless Steel
Stainless Steel Tubing
Steel Service Centers
Titanium
Tungsten
Wire Rope