Fracture mechanics provides a quantitative description of the resistance of a material to fracture. The fracture toughness is a material property which can be used to predict the behaviour of components containing cracks or sharp notches. The fracture toughness properties are obtained by tests on specimens containing deliberately introduced cracks or notches and subjected to prescribed loading conditions.
Cracking Pipe
Depending on the strength of the material and the thickness of the section, either linear-elastic (LEFM) or elastic-plastic fracture mechanics (EPFM) concepts are applied.
The Linear-Elastic Fracture Mechanics Approach
The stress intensity factor KI describes the intensity of the elastic crack tip stress field in a thick, deeply cracked specimen loaded perpendicular to the crack plane.
KI = Y s (1)
where
s is the nominal stress
a is the crack depth
Y is the correction function dependent on the crack and test piece geometry
The critical value of the stress intensity factor for the onset of crack growth is the fracture toughness KIC.
Another material property obtained from linear-elastic fracture mechanics is the energy release rate GI. It indicates how much elastic strain energy becomes free during crack propagation. It is determined according to Equation (2):
GI = p Y2 s2 a / E = K12 / E (2)
where
E is the Young’s modulus.
Analogous to the stress intensity factor, crack growth occurs when GI reaches a critical value GIc.
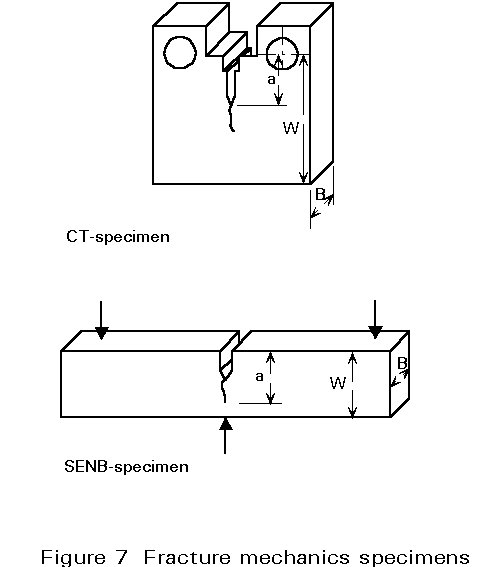
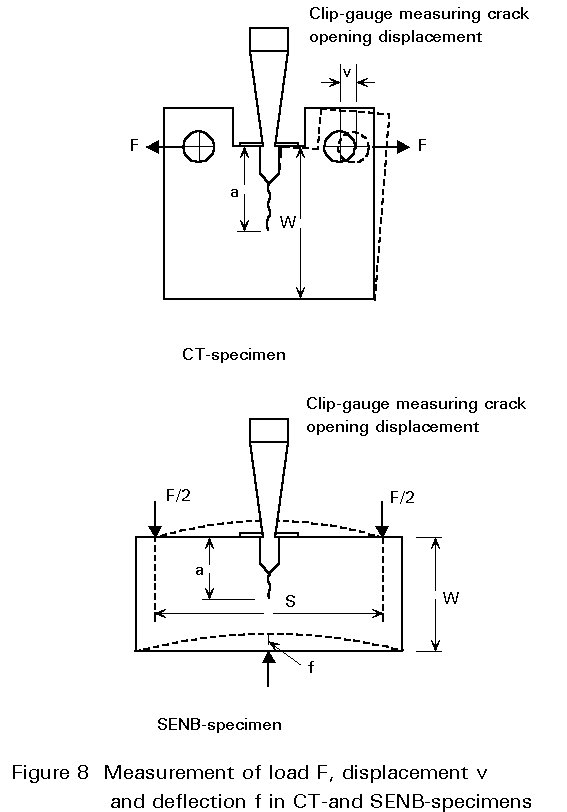
The fracture toughness properties KIc and GIc are determined with fracture mechanics specimens, generally as shown in Figures 7 and 8.
The great value of the fracture toughness parameters KIc and GIc is that once they have been measured for a particular material, Equations (1) and (2) can be used to make quantitative predictions of the size of defect necessary to cause a brittle fracture for a given stress, or the stress which will precipitate a brittle fracture for a defect of known size.
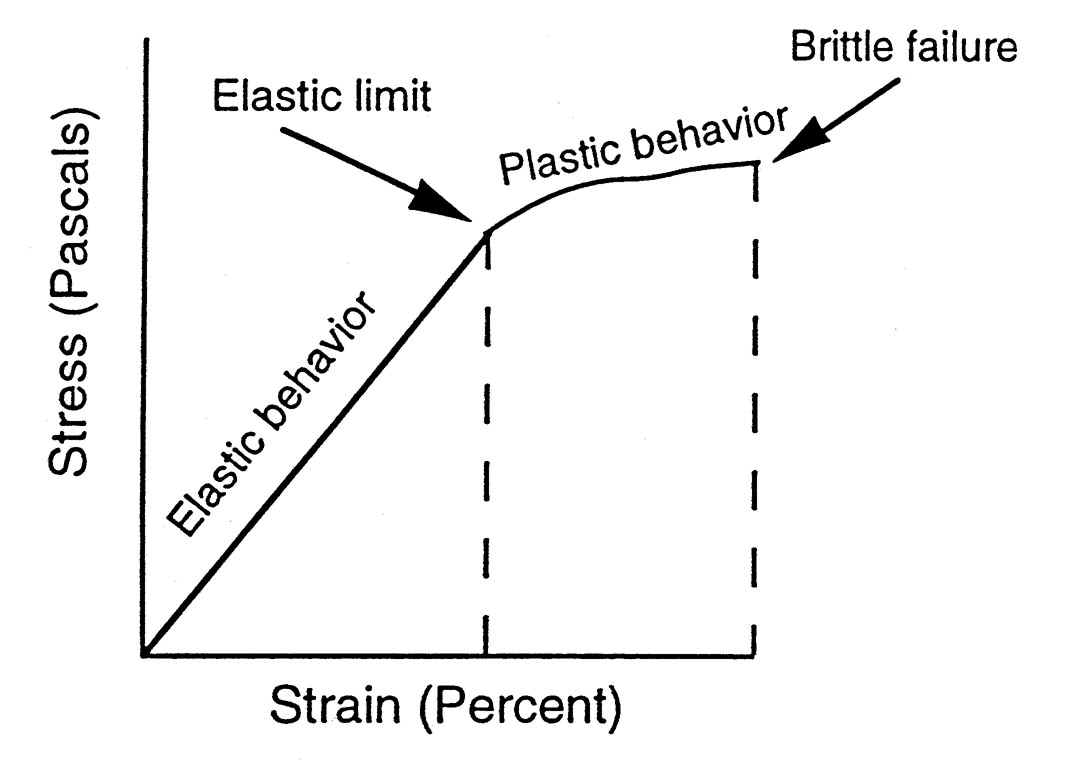
As the designation implies, linear elastic fracture mechanics is applicable to materials which fracture under elastic conditions of loading. The fracture phenomena in high strength quenched and tempered steels are of this type. In lower strength structural steels, extensive plasticity develops at the notch root before failure occurs. This behaviour invalidates many of the assumptions of linear elastic fracture mechanics and makes testing difficult or not meaningful. In such cases elastic-plastic fracture mechanics must be applied.
There are two alternative techniques of elastic-plastic fracture mechanics:
- Crack Tip Opening Displacement (CTOD)
- J Integral
Their essential features are summarised below.
The Elastic-Plastic Fracture Mechanics Approach
A consequence of plasticity developing at the tip of a previously sharp crack is that the crack will blunt and there will be an opening displacement at the position of the original crack tip. This is the crack tip opening displacement (CTOD). As loading continues, the CTOD value increases until eventually a critical value dc is attained at which crack growth occurs.
The critical crack tip opening displacement is a measure of the resistance of the material to fracture, i.e. it is an alternative measurement of fracture toughness. For materials which exhibit little plasticity prior to failure, the critical CTOD, dc, can be related to the linear elastic fracture toughness parameters KIc and GIc as follows:
KIc2 = E.Gk / (1 - u2) = m.E.sy.dc / (1 - u2)
where
E is Youngs modulus
sy is the uniaxial yield strength
u is Poissons ratio
m is a constraint factor having a value between 1 and 3 depending on the state of stress at the crack tip.
Another way of taking account of crack tip plasticity is the determination of the J-integral. J is defined as a path-independent line-integral through the material surrounding the crack tip. It is given by:
J = - (3)
where
U is the potential energy
B is the specimen thickness
a is the crack length
U = (4)
F is the load
Vg is the total displacement
Since the determination of J is difficult, approximate solutions are used in practice.
J = h (5)
where
b = w - a
h = 2 (for SENB-specimens)
h = 2 + 0,522 b/w (for CT-specimens)
The critical value of J is a material characteristic and is denoted JIc. For the linear elastic case, JIc is equal to GIc.
Continue to “Fracture Mechanics Concept“
You might also like
 |
 |
 |
 |
Alloy Suppliers
Aluminum
Aluminum Extrusions
Copper-Brass-Bronze
Nickel
Magnets
Stainless Steel
Stainless Steel Tubing
Steel Service Centers
Titanium
Tungsten
Wire Rope